-- : --
Зарегистрировано — 120 475Зрителей: 63 822
Авторов: 56 653
On-line — 15369Зрителей: 2993
Авторов: 12376
Загружено работ — 2 075 525
«Неизвестный Гений»
облачное асимметричное шифрование
![]() 11 июня ’2018
11 июня ’2018 ![]() 20:15
20:15
Шифрсистемы до сих пор во многом ориентируются на принципе Керкгоффса, или "враг знает систему" (© Шеннон); другими словами, в идеале секретность должна обеспечиваться чем-то таким малым, что можно зажать в кулаке и хранить при себе. В частности, сама схема шифрования должна предполагаться известной возможному злоумышленнику. Принцип был сформулирован в 19-м(!) веке и для своего времени был вполне разумен: меттод шифрования при регулярной переписке можно было понять, а создание специальных шифрующих кабинетов, где сидели бы посвященные в секреты алгоритмов шифровальщики, было бы еще и неудобным. (Ср. историю шифрмашины Энигма, захват которой на подводной лодке привел к взлому всей криптосистемы.) Поэтому сошлись на том, что секретными должны быть только разовые ключи, составленные так, чтобы без знания их расшифровка стала бы практически нереальной. (Заметим, что в особо важных сферах, например, военных, этот принцип стараются избегать, засекречивая всё.)
В 70-х гг. 20-го века начала развиваться модель асимметричного шифрования с открытыми ключами (в частности, на этом построены электронные подписи). Она основана на предположениях(!) о том, что некоторые сложные задачи теории чисел (например, разложение на простые множители) не имеют нетривиального решения; тогда можно построить такие пары ключей, что, зная один сомножитель некоего огромного числа, можно быстро расшифровать текст, тогда как зная лишь всё число, текст можно лишь зашифровать, но не расшифровать.
Но, заметим, что мы живем уже в 21-м веке, когда сильно развиты защищенные облачные вычисления (на серверах; хотя бы банковские сервисы). Так не поправить ли принцип Керкгоффса, изъяв из него положение о предполагаемой известности алгоритма шифрования?
Тогда переписка с открытым ключом будет основана на секретном алгоритме вычисления X по открытому ключу C (зашифровки) закрытого ключа (расшифровки) D: D = X(C). Вычисление производится защищенной программой на сервере.
Начальный этам шифропереписки состоит в получении клиентом пары ключей по запросу на сервер. Облачная программа генерирует открытый ключ C и по нему вычисляет (секретным алгоритмом X) закрытый ключ D. Оба выдаются клиенту.
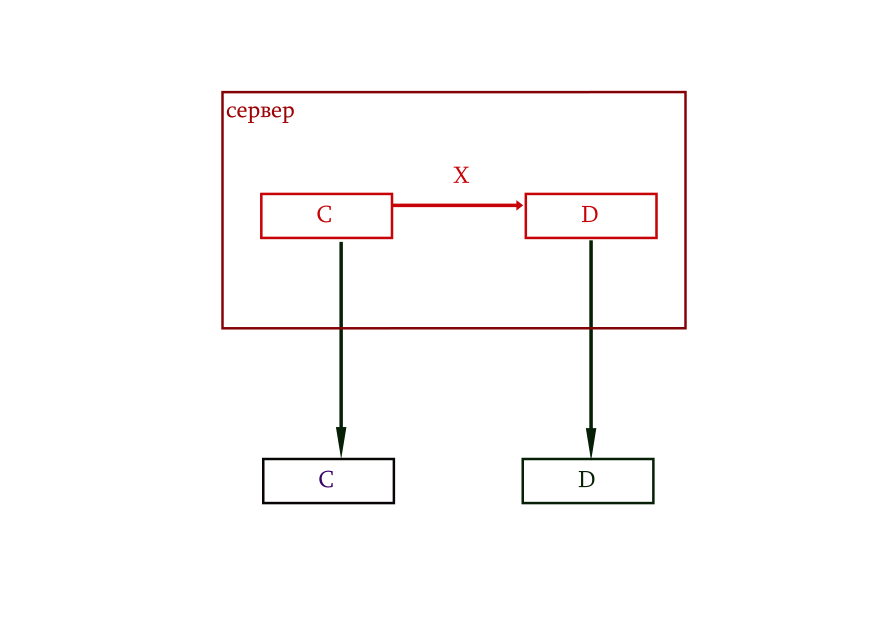
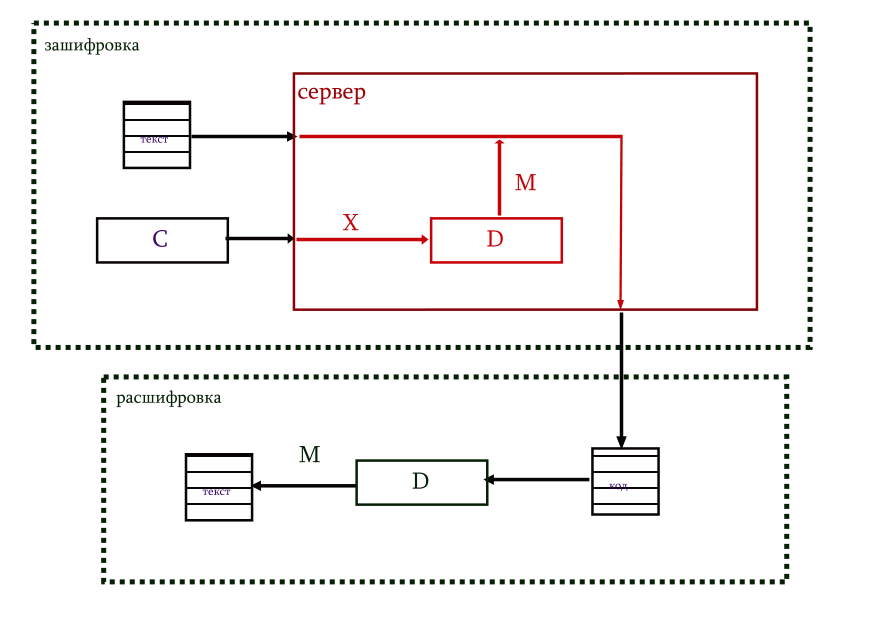
Для шифропереписки открытый ключ высылается корреспонденту. Шифрование происходит через обращение к стандартному лицензионному серверу, которому предоставляется исходный текст и открытый ключ. Облачная программа по открытому ключу вычисляет закрытый, после чего шифрует с его помощью исходный текст каким-нибудь стандартным симметричным алгоритмом шифрования M. (То есть, наивный, думает, что шифрование идет по его ключу, а на самом деле оно производится совсем по другому!)
Расшифровка производится просто: тем же стандартным алгоритмом M по закрытому ключу. Она даже не требует обращения к серверу.
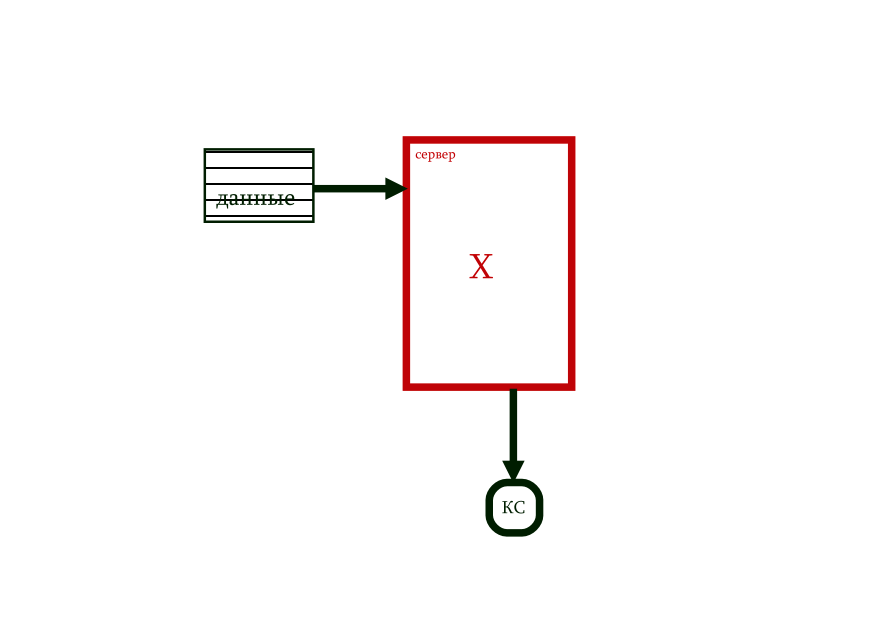
Ну а электронная подпись, скрепляющая данные, становится вообще простой процедурой. Стандартный лицензированный сервер секретным алгоритмом вычисляет контрольную сумму, которая и становится гарантией целостности документа. Для проверки надо будет просто еще раз через сервер ее вычислить, сверив с имеющейся.
Заметим, что существующие системы шифрования с открытым ключом всё равно пришли к сложной облачной системе доверительного сертифицирования, что само по себе является аргументом в пользу пересмотра принципа Керкгоффса.
Итак, предлагается перенести часть секретности на облачный алгоритм шифрования.
Достоинства.
1. Простота реализации. Пара ключей получается более простыми алгоритмами, нежели решение сложных арифметических задач.
2. Отпадает надобность в сложной системе сертификации ключей.
3. Надежность. Стойкость алгоритма может быть достаточно достоверно оценена. Тогда как существующие методы в массе своей основаны на предположениях об отсутствии эффективных методов решения сложных задач.
Недостатки.
Переписка и получение электронной подписи может производиться только он-лайн, через обращение к серверу.
В 70-х гг. 20-го века начала развиваться модель асимметричного шифрования с открытыми ключами (в частности, на этом построены электронные подписи). Она основана на предположениях(!) о том, что некоторые сложные задачи теории чисел (например, разложение на простые множители) не имеют нетривиального решения; тогда можно построить такие пары ключей, что, зная один сомножитель некоего огромного числа, можно быстро расшифровать текст, тогда как зная лишь всё число, текст можно лишь зашифровать, но не расшифровать.
Но, заметим, что мы живем уже в 21-м веке, когда сильно развиты защищенные облачные вычисления (на серверах; хотя бы банковские сервисы). Так не поправить ли принцип Керкгоффса, изъяв из него положение о предполагаемой известности алгоритма шифрования?
Тогда переписка с открытым ключом будет основана на секретном алгоритме вычисления X по открытому ключу C (зашифровки) закрытого ключа (расшифровки) D: D = X(C). Вычисление производится защищенной программой на сервере.
Начальный этам шифропереписки состоит в получении клиентом пары ключей по запросу на сервер. Облачная программа генерирует открытый ключ C и по нему вычисляет (секретным алгоритмом X) закрытый ключ D. Оба выдаются клиенту.

Для шифропереписки открытый ключ высылается корреспонденту. Шифрование происходит через обращение к стандартному лицензионному серверу, которому предоставляется исходный текст и открытый ключ. Облачная программа по открытому ключу вычисляет закрытый, после чего шифрует с его помощью исходный текст каким-нибудь стандартным симметричным алгоритмом шифрования M. (То есть, наивный, думает, что шифрование идет по его ключу, а на самом деле оно производится совсем по другому!)
Расшифровка производится просто: тем же стандартным алгоритмом M по закрытому ключу. Она даже не требует обращения к серверу.

Ну а электронная подпись, скрепляющая данные, становится вообще простой процедурой. Стандартный лицензированный сервер секретным алгоритмом вычисляет контрольную сумму, которая и становится гарантией целостности документа. Для проверки надо будет просто еще раз через сервер ее вычислить, сверив с имеющейся.

Заметим, что существующие системы шифрования с открытым ключом всё равно пришли к сложной облачной системе доверительного сертифицирования, что само по себе является аргументом в пользу пересмотра принципа Керкгоффса.
Итак, предлагается перенести часть секретности на облачный алгоритм шифрования.
Достоинства.
1. Простота реализации. Пара ключей получается более простыми алгоритмами, нежели решение сложных арифметических задач.
2. Отпадает надобность в сложной системе сертификации ключей.
3. Надежность. Стойкость алгоритма может быть достаточно достоверно оценена. Тогда как существующие методы в массе своей основаны на предположениях об отсутствии эффективных методов решения сложных задач.
Недостатки.
Переписка и получение электронной подписи может производиться только он-лайн, через обращение к серверу.
Комментарии:
Оставлять сообщения могут только зарегистрированные пользователи
Трибуна сайта
Наш рупор




